이진 검색트리의 한계
이진 검색 트리는 운이 나쁘면 트리의 균형을 이루지 못함
이진 검색 트리는 삽입, 검색, 삭제 연산의 시간 복잡도가 트리의 높이(h)에 비례한다.
예시 트리:
1
\
2
\
3
\
4
\
5
이러한 경우 작업시간은 배열과 동일하다. (평균 n의 수행시간)
이런 경우를 피하기 위해 고안해 낸 것이 균형 이진 검색트리이다.
균형 검색 트리란?
이진 트리의 균형이 잘 맞도록 유지해서 검색, 삽입, 삭제 잡업들의 수행시간을 최대 logn의 시간을 보장한다.
AVL 트리
특징
- 최초의 균형 검색 트리 (1962년 개발)
- 각 노드에 대해 왼쪽 서브트리 높이와 오른쪽 서브트리 높이의 차이가 1을 넘지 않도록 유지.
- 삽입/삭제 시 불균형이 발생하면 회전 연산을 통해 균형을 회복.
- Adelson-Velskii와 Landis에 의해 고안됨.
30
/ \
20 40 (초기 AVL 트리) - 높이 차이 : 0
30
/ \
20 40
/
10 (10을 삽입) - 높이 차이 : 1
30
/ \
20 40
/
10
/
5 (5를 삽입) - 높이 차이 : 2(균형 깨짐)
수선 기준이 되는 노드(30)를 중심으로 한번 우회전하여 불균형 해소
20
/ \
10 30
/ \
5 40
- 위와 같은 사례는 한번의 좌회전 혹은 우회전으로 균형의 불균형이 해소 되는 경우이다.
불균형의 유형에는 4가지가 존재한다.
- LL 타입 : t.left.left가 가장 깊음.
30
/
20
/
10
불균형 해결 방법: 단일 우회전
20
/ \
10 30
- LR 타입 : t.left.right가 가장 깊음
30
/
20
\
25
불균형 해결 방법: 20을 기준으로 좌회전 후 LL타입으로 변경 후 30을 기준으로 우회전
1. 좌회전(20 기준)
30
/
25
/
20
2. 우회전(30 기준)
25
/ \
20 30
- RR 타입 : t.right.right가 가장 깊음
30
\
40
\
50
불균형 해결 방법 : 단일 좌회전
40
/ \
30 50
- RL 타입 : t.right.left가 가장 깊음
30
\
50
/
40
불균형 해결 방법 : 50을 기준으로 우회전 후 R타입으로 변경 후 30을 기준으로 좌회전
1. 우회전(50기준)
30
\
40
\
50
2. 좌회전(30기준)
40
/ \
30 50
LL 타입과 RR 타입은 한 번의 회전으로 불균형이 해결되지만
LR 타입과 RL타입은 두번의 회전이 필요하다.
우회전을 예시로 들자면 중심이 되는 노드의 왼쪽의 좌서브 트리는 깊이가 한칸 낮아지고 왼자식의 우서브트리(LR 서브트리)는 깊이가 유지되는 성질 때문에 이런 차이가 발생한다.
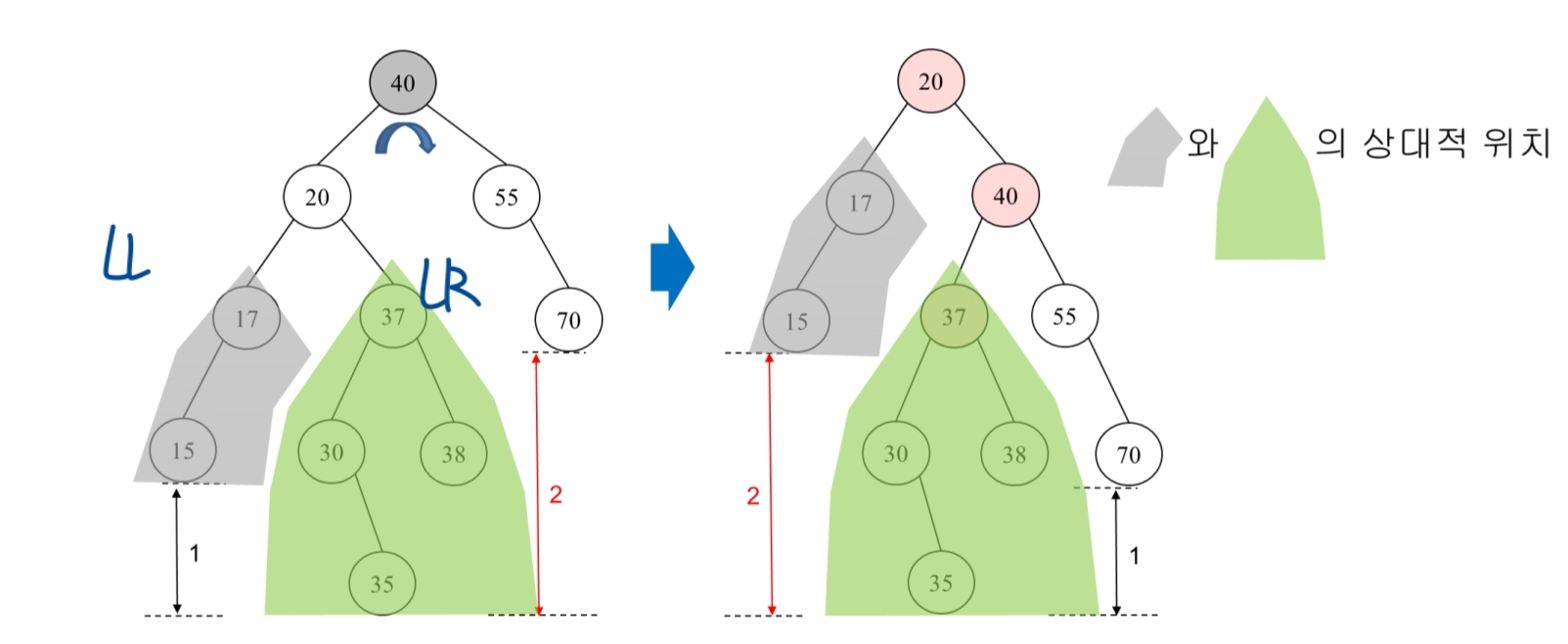
그러므로 우회전 할 때는 항상 LL 서브트리가 LR 서브트리보다 깊이가 더 얕지 않도록 해야한다.
calss AVLNode: # AVL 트리의 노드를 저장하기위한 클래스
def __init__(self, newItem, left, right, h):
self.item = newItem
self.left = left
self.right = right
self.height = h
class AVLTree: # AVL 자료구조를 관리하기 위한 클래스
def __init__(self):
self.NIL = AVLNode(None, None, None, 0)
self.__root = self.NIL
self.LL = 1
self.LR = 2
self.RR = 3
self.RL = 4
self.NO_NEED = 0
self.ILLEGAL = -1
검색
def search(x): # 트리에서 값 x를 검색
return __searchItem(self.__root, x) # 루트 노드부터 시작
def __searchItem(self, tNode, x):
if tNode == self.NIL: # 값을 찾지 못한 경우
return self.NIL # 검색 실패 NIL 반환
elif x == tNode.item: # 검색하는 값이 현재 노드의 값과 같은경우
return tNode # 현재 노드 반환
elif x < tNode.item: # x가 현재노드의 값보다 작은 경우
return __searchItem(tNode.left, x) # 좌 서브트리로 이동해서 검색
else: # x가 현재노드의 값보다 큰 경우
return __searchItem(tNode.right, x) # 우 서브트리로 이동해서 섬색삽입
def insert(x):
return __searchItem(self.__root, x)
def __insertItem(self, tNode, x):
if tNode == self.NIL: # 빈트리에 넣거나 리프노드에 삽입하는 경우
tNode = AVLNode(x,self.NIL, self.NIL, 1) # 새노드를 생성하고 높이를 1로 설정
elif x < tNode.item: # 삽입하고자 하는 값이 현재 노드 값보다 작은경우
tNode.left = self.__insertItem(tNode.left, x) # 왼쪽 서브트리에 삽입
tNode.height = 1 + max(tNode.right.height, tNode.left.height) # 높이 갱신
type = self.__needBalance(tNode) # 균형상태 확인
if type != self.__needBalance(tNode): # 균형이 무너진 경우
tNode = self.__balanceAVL(tNode, type) # 조정 진행
else: # 삽입하고자 하는 값이 현재 노드 값보다 큰 경우
tNode.right = self.__insertItem(tNode.right, x) # 오른쪽 서브트리에 삽입
tNode.height = 1 + max(tNode.right.height, tNode.left.height) # 높이 갱신
type = self.__needBalance(tNode) # 균형상태 확인
if type != self.NO_NEED: # 균형이 무너진 경우
tNode = self.__balanceAVL(tNode, type) # 조정 진행
return tNode # 삽입 및 조정 후 현재 노드 반환삭제
def delete(self, x):
self.__root = self.__deleteItem(self.__root, x)
def __deleteItem(self, tNode, x):
if tNode == self.NIL: # 삭제하려는 값이 존재하지 않는 경우
return self.NIL # NIL 반환
else: # 삭제하려는 값이 찾음
if x == tNode.item:
tNode = self.__deleteNode(tNode) # 해당 노드를 삭제하고 트리 구조를 갱신
elif x < tNode.item: # 삭제하려는 값이 현재 노드보다 작은 경우
tNode.left = self.__deleteItem(tNode.left, x) # 왼쪽 서브트리에서 삭제 수행
tNode.height = 1 + max(tNode.right.height,tNode.right.height) # 높이 갱신
type = self.__needBalance(tNode) # 균형 상태 확인
if type != self.NO_NEED: # 조정이 필요한 경우
tNode = self.__balanceAVL(tNode,type) # 조정 수행
elif x > tNode.item: # 삭제하려는 값이 현재 노드보다 큰 경우
tNode.right = self.__deleteItem(tNode.right, x) # 오른쪽 서브트리에서 삭제 수행
tNode.height = 1 + max(tNode.right.height, tNode.left.height) # 높이 갱신
type = self.__needBalance(tNode) # 균형 상태 확인
if type != self.NO_NEED: # 균형 조정이 필요한 경우
tNode = self.__balanceAVL(tNode, type) # 균형 회복 수행
return tNode # 삭제 및 균형 조정 후, 갱신된 현재 노드를 반환
def __deleteNode(self, tNode):
if tNode.left == self.NIL and tNode.right == self.NIL: # 삭제할 노드에 자식이 없는 경우
return self.NIL
elif tNode.left == self.NIL: # 오른쪽 자식 노드만 있는 경우
return self.right # 오른쪽 자식 노드와 부모노드를 직접 연결
elif tNode.right == self.NIL: # 왼쪽 자식 노드만 있는 경우
return self.left # 왼쪽 자식 노드와 부모노드를 직접 연결
else: # 두 자식 노드가 존재하는 경우
(rtnItem, rtnNode) = self.__deleteMinItem(tNode.right) # 우 서브트리에서 최솟값을 찾아 대체
tNode.item = rtnItem # 우 서브트리의 최솟값으로 변경
tNode.right = rtnNode # 오른쪽 서브트리 갱신
tNode.height = 1 + max(tNode.right.height, tNode.left.height) # 높이 갱신
type = self.__needBalance(tNode) # 균형상태 확인
if type != self.NO_NEED: # 조정이 필요한경우 조정 실행
tNode = self.__balanceAVL(tNode,type)
return tNode # 갱신된 노드 반환
def __deleteMinItem(self, tNode):
if tNode.left == self.NIL: # 최솟값을 찾은 경우(좌 자식노드가 없음)
return (tNode.item, tNode.right) # 해당 노드의 값과 우 자식노드 반환
else: # 왼 자식노드가 존재하면 재귀적으로 왼 서브트리에서 최솟값 찾기
(rtnItem, rtnNode) = self.__deleteMinItem(tNode.left) # 왼쪽 서브트리에서 최솟값을 삭제한 후, 현재 노드의 왼쪽 자식을 갱신
tNode.left = rtnNode
tNode.height = 1 + max(tNode.right.height, tNode.left.height) # 높이 갱신
type != self.__needBalance(tNode) # 조정이 필요한 경우 조정진행
if type != self.NO_NEED:
tNode = self.__balanceAVL(tNode, type)
return (tNode, rtnItem) # 갱신된 현재 노드와 삭제된 최솟값을 반환
균형잡기
def __balanceAVL(self, tNode,type): # 각 타입에 맞게 조정
return Node = self.NIL
if type == self.LL:
return Node =self.__rightRotate(tNode)
elif type == self.LR:
tNode.left = self.__leftRotate(tNode.left)
return Node = self.__rightRotate(tNode)
elif type == self.RR:
return Node = self.__leftRotate(tNode)
elif type == self.RL:
tNode.right = self.__rightRotate(tNode.right)
return Node = self.__leftRotate(tNode)
else:
print('조정불가능')
return Node
def __leftRotate(self, t): # 좌회전
RChild = t.right # 현재 노드의 오른쪽 자식 가져오기
if RChild == self.NIL:
print(t.item,'''s RChild Shouldn't be NIL'')
RLChild = RChild.left # 오른쪽 자식노드의 왼쪽 자식을 가져오기
RChild.left = t # 현재 노드를 새로운 부모 노드의 왼쪽 자식으로 설정
t.right = RLChild # 현재 노드의 오른쪽 자식을 기존 RChild의 왼쪽 자식으로 설정
t.height = 1 + max(RChild.right.height, RChild.left.height) # 높이갱신
return RChild # 좌회전 후 새로운 루트노드를 반환
def __rightRotate(self, t): # 우회전
LChild = t.left # 현재 노드의 왼쪽 자식 가져오기
if LChild == self.NIL:
print(t.item,'''s LChild shouldn't be NIL'')
LRChild = LChild.right # 왼쪽 자식의 오른쪽 자식을 가져오기
LChild.right = t # 현재 노드를 새로운 부모 노드의 오른쪽 자식으로 설정
t.left = LRChild # 현재 노드의 왼쪽 자식을 기존 LChild의 오른쪽 자식으로 설정
t.height = 1 + max(RChild.right.height, RChild.left.height) # 높이갱신
return LChild # 우회전 후 새로운 루트노드를 반환
def __needBalance(self,t):
type = self.ILLEGAL
if (t.left.height + 2 <= t.right.height): # R유형
if (t.right.left.height) <= (t.right.right.height):
type = self.RR
else:
type = self.RL
elif (t.left.height >= t.right.height +2): # L유형
if (t.left.left.height) >= (t.left.right.height):
type = self.LL
else:
type = self.LR
else:
type = self.NO_NEED
retutn type'[자료 구조 및 알고리즘]' 카테고리의 다른 글
| [자료구조 및 알고리즘] 그래프 (2) | 2024.12.07 |
|---|---|
| [자료구조 및 알고리즘] 해시 테이블 (0) | 2024.12.04 |
| [자료구조 및 알고리즘] 색인과 이진 검색 트리 (0) | 2024.12.03 |
| [자료구조 및 알고리즘] 고급 정렬 (0) | 2024.12.01 |
| [자료구조 및 알고리즘] 기본 정렬 (0) | 2024.12.01 |


