그래프
: 그래프는 현상이나 사물을 정점과 간선으로 표현한 것, 정점은 대상이나 개체를 나타내고 간선은 이들 간의 관계를 나타낸다.
그래프 G = (V, E) , V는 정점들의 집합, E는 간선들의 집합
그래프의 종류
- 그래프(무향 그래프) : 관계의 존재 여부 표시
- 가중 그래프 : 관계의 정도를 간선에 가중치를 주어 나타냄
- 방향 그래프 : 각 정점의 관계를 방향성을 가진 간선으로 표시
- 가중 방향 그래프 : 방향성을 가진 간선에 가중치를 주어 나타냄
그래프 표현 방법에는
- 인접 행렬 : 이해하기 쉽고 간선의 존재 여부를 즉각 알 수 있음, n^2의 공간이 필요하다. 간선의 밀도가 아주 높은 그래프에서는 적합, 그렇지 않으면 거의 다 0으로 채워짐
- 인접 리스트 : 각 정점마다 연결 리스트를 만듦, 행렬에 비해 공간 낭비가 없다. 하지만 거의 모든 정점 쌍에 대해 간선이 존재하는 경우에는 오히려 연결 리스트의 링크 정보를 표현하기 위한 오버헤드 발생
- 인접 배열 : 리스트 대신 배열을 사용하면 리스트의 링크를 위한 공간을 절약할 수 있다. 그래프가 변하지 않는 정적이라면 리스트보다 배열이 효율적이다.
- 인접 해시 테이블 : 노드 접근과 검색에는 효율적이지만 배열보다 추가 공간이 필요하여 밀집 그래프에는 비효율적이다.
그래프의 순회
순회란 그래프의 한 정점에서 시작하여 도달 가능한 모든 정점을 방문하는 것을 그래프 순회라고 한다.
너비 우선 탐색(Breadth – First Search)
방문 순서 : 루트 , 루트의 자식, 루트에서 2개의 간선을 거쳐 도달할 수 있는 정점, 루트에서 3개의 간선을 거쳐 도달 할 수 있는 정점…..

큐를 이용 : 정점을 첫 방문할 때 큐에 삽입하고, 큐에서 정점을 하나씩 빼가면서 거기서 연결된 정점들을 큐에 삽입
먼저 삽입된 노드를 먼저 순회한다.(First in First out), 큐를 이용
깊이 우선 탐색(Depth – First Search)
방문순서 : 루트, 루트의 자식, 루트의 자식의 자식….. 더 이상 내려갈 곳이 없으면 위로 되돌아 와서 내려갈 수 있는 곳으로 내려감

스택 이용 : 정점을 첫 방문할 때 스택에 삽입하고, 더 이상 할 일이 없을 때 스택에서 삭제
더 이상 내려갈 곳이 없을 때마다 빽 트래킹을 해야한다.(Last in First out) 스택을 이용
최소 신장 트리
: 가중치가 있는 무향 그래프로 만들 수 있는 모든 신장 트리 중 비용이 가장 낮은 트리
신장 트리 비용은? 신장 트리를 구성하는 간선 가중치의 합
최소 신장 트리의 조건
- 무향 연결 그래프
- 싸이클이 존재하지 않는다(리프에서 노드로 왔던길을 다시 가지 않고는 못간다)
- 최소한의 간선(정점의 수 -1)
- 최소 신장 트리를 찾는 방법
1. 프림 알고리즘 : 하나의 정점 집합을 점점 키워 나가는 방식
2. 크루스칼 알고리즘 : 여러 정점 집합으로 시작해서 집합들을 합쳐 나가는 방식
프림 알고리즘
아무 간선도 없는 상태에서 간선을 하나씩 더해가는 작업을 v(정점의 수) - 1 번한다.
이를 구현하는 수단으로 정점 집합 S를 운용하여 정점 하나에서 시작하여 한 번에 하나씩 더해 간다.
집합 S에 포함된 정점이랑 연결된 간선의 가중치가 가장 작은 간선이랑 연결된 정점을 집합 S에 추가한다.


정점이 집합에 추가될 때마다 연결비용이 작은 값으로 초기화 되는 가정이 포함
위상 정렬
:성질을 만족하는 순서로 작업을 정렬하는 것
싸이클이 없는 방향 그래프에서 모든 정점을 정렬하되 방향을 고려(우선 순위가 있음)

선택된 정점과 연결된 간선은 제거하고 진입간선이 없는 정점중에서 선택가능
최단 경로(Shortest Path)
1. 다익스트라 알고리즘: 모든 간선 가중치가 음이 아님
2. 벨만-포드 알고리즘: 음의 가중치를 허용하되 음의 싸이클은 허용하지 않음 - 음의 가중치? 해당 경로를 지났을 때 어드벤티지를 주고 싶을 때 사용
다익스트라 알고리즘과 프림 알고리즘의 차이(중요)
프림 알고리즘은 정점 사이의 간선 비용이 가장 작은걸 선택
다익스트라 알고리즘은 시작 정점에서 해당정점까지 가는데 총 비용을 고려해서 최소를 선택

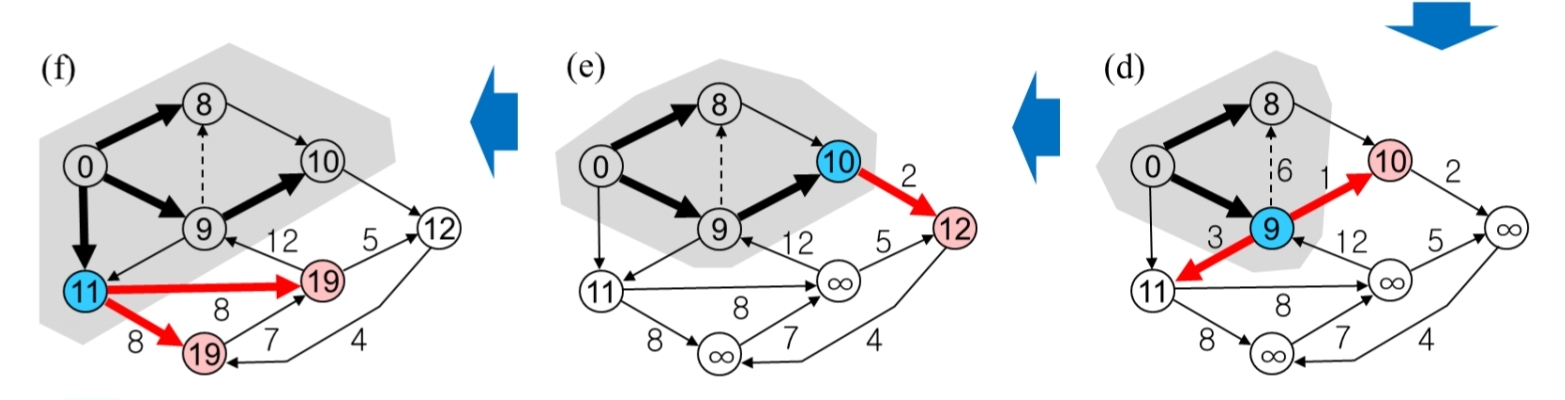
프림 알고리즘과 동일하게 정점이 추가 될 수록 가능한 비용의 최솟값으로 초기화하는 과정 포함
'[자료 구조 및 알고리즘]' 카테고리의 다른 글
| [자료구조 및 알고리즘] 해시 테이블 (0) | 2024.12.04 |
|---|---|
| [자료구조 및 알고리즘] 균형 검색 트리 - AVL 트리 (0) | 2024.12.04 |
| [자료구조 및 알고리즘] 색인과 이진 검색 트리 (0) | 2024.12.03 |
| [자료구조 및 알고리즘] 고급 정렬 (0) | 2024.12.01 |
| [자료구조 및 알고리즘] 기본 정렬 (0) | 2024.12.01 |


