해시 테이블
선형 자료구조(리스트, 스택, 큐)
색인 자료구조(검색 트리, 해시 테이블)
앞서 정리한 검색트리와 함께 색인 자료구조이다.
왜? 사용할까?
배열 또는 리스트는 평균 n의 수행시간이 소요된다.
이를 색인을 이용해서 더 빠르게 처리하기 위해 이진 검색 트리를 사용한다.
이진 검색트리는 검색, 삽입, 삭제에 평균 logn의 수행시간이 소요되고 최악의 경우 n의 수행시간이 소요된다.
이진 검색트리에서 최악의 경우는 한쪽으로만 트리가 치우치는 경우이다.
10
\
20
\
30
\
40 이러한 경우에는 이진 검색트리임에도 불구하고 수행시간이 단순 연결 리스트와 동일해진다.
최악의 경우를 방지 하기위해 서브트리들 사이의 높이의 균형을 맞추는 균형 이진트리가 있다.
균형 이진 트리는 최악의 경우에도 평균 logn 의 수행시간을 가진다.
여기서 더 발전시켜 수행시간이 평균 1인 자료구조가 바로 해시테이블이다.
- 검색트리는 키가 저장될 자리를 이미 트리에 존재하는 키와 비교하여 상대적으로 결정
vs
- 해시 테이블은 키가 저장될 자리를 키의 값으로 결정(키끼리 비교하는 것이 아니라 자신의 킷값에 의해 위치가 결정)
해시 테이블은 아주 빠른 검색, 삽입, 삭제 작업을 제공
디자인 철학에 맞게 디자인하여 저장된 자료와 양의 상관없이 평균 상수 시간 작업, 즉 수행시간이 평균 1
이론적으로 색인 효율의 극한에 위치
해시 함수와 해시 테이블
임의의 키를 해시 테이블에 저장하려면 해당 키의 해시 값을 계산해야 한다.
해시 값을 어떻게 계산할까? > 해시함수에 의해서
- 해시 테이블이 총 m개의 키를 저장할 수 있다면 테이블의 각 자리는 0부터 m-1의 주소 값을 가진다.
- 해시 함수는 임의의 키 값을 입력으로 받아 0,1,2,...,m-1(주소) 중 한 값으로 리턴한다.
- 해시 함수는 서로 다른 두 키가 한 주소를 놓고 충돌할 확률을 낮추며, 입력키를 해시 테이블 전체에 고루 분산시켜 저장해야 한다.
1. 나누기 방법
나누기 방법은 해시 테이블 크기보다 큰 수를 해시 테이블 크기 범위에 들어오도록 수축시킨다.
h(x) = x%m , x는 키값, % 나누기 연산자, m은 해시 테이블 크기
- m은 2의 멱수에 가깝지 않은 소수를 권장
- 만일 m=2^p라면 입력 키의 하위 p비트에 의해 해시 값이 결정되므로 해시 값을 분산시키기에 이상적이지 않다.
- 해시 값은 입력 키의 모든 비트를 이용하는 것이 확률적으로 좋은 분포를 가진다.

2. 곱하기 방법
곱하기 방법은 먼저 입력 값을 0과 1사이의 소수로 대응시킨 다음 해시 테이블 크기 m을 곱하여 0부터 m-1 사이로 팽창키긴다.
h(x) = (xA % 1)*m , x는 키값, % 나누기 연산자, 0<A<1, m은 해시 테이블 크기
- 키값(x)에 A를 곱한 다음 소수부만 취한다
- m을 곱한 뒤 정수부만 취한다.
결과적으로 곱하기 방법은 나누기 방법과 달리 해시 테이블의 크기 m을 아무렇게나 잡아도 상관 없다.
2^p 가 컴퓨터 이진수 환경에 맞게 자연스럽다.

충돌해결
충돌이란 서로 다른 두 개 이상의 키가 같은 해시 값을 가지게 되는 상황
충돌을 해결하는 방법 첫번째 체이닝
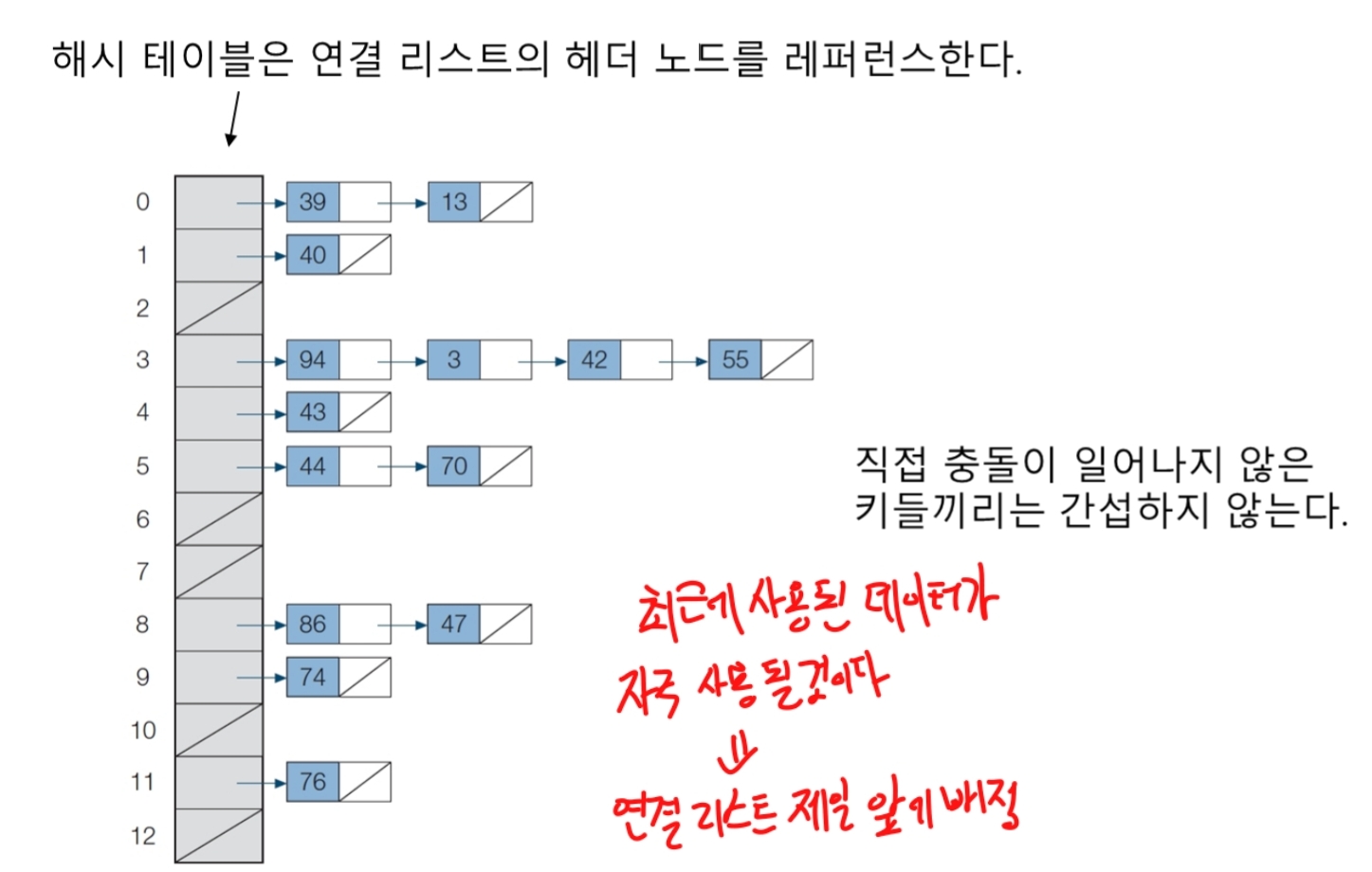
체이닝
같은 주소로 해싱되는 키를 모두 하나의 연결 리스트에 매달아 관리
해시 테이블 크기가 m이면 최대 m개의 연결 리스트가 존재 할 수 있다.
from list.CircularlinkedList import *
from list.listNode import *
class ChainedHashTable:
def __init__(self, n):
self.__table = [CircularLinkedList() for i in range(n)] # 충돌이 발생한 경우 동일한 해시 값의 항목을 저장하는 체이닝
self.__numItems = 0; # 해시 테이블에 저장된 총항목 수를 추적하기 위한 변수
def __hash(self, x) # 해시함수
return x % len(self.__table) # 나누기 방법 사용
def insert(self, x): # 삽입구현
slot = self.__hash(x) # 해시함수를 이용하여 slot값 부여
self.__table[slot].insert(0,x) # 체이닝 맨앞에 삽입(최근에 입력된것을 앞에 삽입)
self.__numItems += 1 # 리스트안에 원소 수 1 추가
def search(self, x):
slot = self.__hash(x) # 키값을 슬롯 값으로 변환
if self.__table[slot].isEmpty(): # 해당 체이닝이 비었는지 확인
return None
else:
head = prev = self.__table[slot].getNode(-1) # 원형 리스트에서 헤드부터 시작해서 다시 헤드가 나올때 까지 탐색
curr = prev.next
while curr != head:
if curr.item == x: # 해당 값을 찾으면 리턴
return curr
else:
prev = curr
curr = curr.next
return None
개방 주소 방법
개방 주소 방법은 체이닝과 달리 추가 공간을 사용하지 않는다.
충돌이 일어나면 어떻게라도 주어진 테이블 공간에서 해결함
개방 주소 방법에서의 임의의 키를 테이블에 삽입하는 과정
1. 해시함수 계산
2. 계산된 주소에 다른 키가 없으면 그 자리에 넣는다
3. 그 자리에 다른 키가 있으면 충돌이 발생한 경우이다
- 이러한 경우는 정해진 규칙에 의해 다음 자리를 찾는데 빈자리가 나올 때까지 계속 찾는다(순차적 해시 함수)
- 처음 계산한 해시 함수를 0번 해시 함수
- 충돌이 일어나서 다음 주소를 계산하는 것을 1번 해시 함수
- 또 충돌이 일어나서 다음 주소를 계산하는 것을 2번 해시함수
- h0(x), h1(x), h2(x), ...... 이처럼 해시함수를 여러개 사용
개방 주소 방법은 테이블에 주어진 공간만 사용 할 수 있으므로 적재율이 1을 넘을 수 없음
충돌 해결 방법
1. 선형 탐색 : 1차 함수 이용
선형 탐색은 가장 간단한 충돌 해결 방법으로 충돌이 일어난 바로 뒷자리를 본다.
$$ h_{i}(X) = (h_{0}(x) + 1) % m $$
해시값이 이미 존재하는 경우 해시 값에 1을 더해서 동일한 해시함수 값을 도출
테이블의 경계를 넘어갈 경우에는 맨앞으로 가면 됨
선형 탐색은 특정 영역에 키가 몰릴 때 치명적으로 성능이 떨어진다. 이러한 현상을 1차 군집이라 한다.

2. 이차원 탐색 : 2차 함수 이용
이차원 참색은 바로 뒷자리(선형탐색)를 보는 대신 보폭을 이차 함수에 의해 넓혀가면서 봄
$$ h_{i}(X) = (h_{0}(x) + i^2) % m $$
이차 함수를 쓰면 1차 군집이 생겨 특정 영역에 키가 몰려도 그 영역을 빨리 벗어날 수 있다.
그러나, 여러 개의 키가 동일한 초기 해시 함수값(h0())을 가지면 모두 같은 순서로 탐색하게 되므로 비효율을 피할 수 없다.
이러한 현상을 2차 군집이라고 한다.

3. 더블 해싱 : 서로 다른 2개 함수 이용
더블 해싱은 2개의 함수를 사용함
$$ h_{i}(X) = (h_{0}(x) + i*f(x)) % m $$
보조 해시 함수 f(x)를 사용
h(x)와 f(x)는 서로 다른 함수이다. 따라서 충돌이 생겨 다음에 볼 주소를 계산할 때 두번째 해시 함수값 만큼씩 점프한다.
그러므로 2차 군집 문제가 발행하지 않는다.

class HashOpenAddressed:
def __init__(self, n):
self.__table = [None for i in range(n)] # 크기가 n인 테이블 생성
self.__numItem = 0 # 테이블에 저장된 항목 수 저장항목
self.__DELETED = -54321 # 삭제된 항목을 표시하기 위해 사용하는 특별한 값 슬롯에 값이 없는경우 None 삭제된 경우 self.__DELETED
def __hash(self, i, x): # 해시 함수
return (x + i) % len(self.__table) # 선형탐사방법 사용
def insert(self, x): # insert 구현
if self.__numItems == len(self.__table): # 테이블에 저장된 항목수와 테이블 길이가 같은경우(테이블 꽉참)
print('error') # 에러
else: # 테이블에 남은 공간이 있다면
for i in range(len(self.__table)): # 탐사
slot = self.__hash(i, x) # 해시값 만들어서 찾기
if self.__table[slot] == None or self.__table[slot] == self.__DELETED: # 테이블에 해당 해시 값이 비어있거나 삭제된경우
self.__table[slot] = x # 해당 해시값에 값 저장
self.__numItems += 1 # 테이블에 원소 수 추가
break
NOT_FOUND = -12345 # 상수 설정
def search(self, x): # search 구현
for i in range(len(self.__table)): # 탐사
slot = self.__hash(i, x) # 해시 값 변환
if self.__table[slot] == None: # 해당 해시값에 테이블이 비어있는 경우
return HashOpenAddressed.NOT_FOUND
if self.__table[slot] == x: # 검색하는 값을 찾은 경우
return slot # 슬롯 반환
return self.__NOT_FOUND # x가 발견되지 않은경우
def delete(self, x): # delete 구현
for i in range(len(self.__table)): # 탐사
slot = self.__hash(i, x) # 해시 값 변환
if self.__table[slot] == None: # 테이블에 해당 해시값이 비어있는경우
break # 삭제할 값이 없으므로 끝
if self.__table[slot] = x: # 삭제할 값을 찾음
self.__table[slot] == self.__DELETED # 해당 해시에 삭제 표시
self.__numItems -= 1 # 테이블에 원소 수 줄이기
break
해시테이블에서 고려사항
1. 삭제 시 주의할 점(중요)
테이블에 해당 해시 값이 비어있는 경우는 None, 해당 해시 값이 원래 존재했다가 삭제된 경우 상수 DELETED를 할당한다
왜?
만약 똑같이 None으로 처리한다면
검색을 통해서 해시 테이블을 탐색하다가 빈공간을 발견했다 실제로 찾는 값이 없는지? 다음 해시값에 찾는 값이 있지만 앞에 해시 값이 삭제 된것인지? 판단 불가!!!!

2. 적재율
해시 테이블에서 원소가 차 있는 비율은 해시 테이블의 성능에 매우 중요한 영향을 미친다
적재율은 보통 a로 표현. a = n/m (n : 원소 총 수, m : 테이블 크기)
a값이 크면 해시 테이블의 성능이 나빠진다, 특히 개방 주소 방법에서
따라서, 상한 기준을 설정한 다음 이를 넘으면
- 테이블 크기를 대략 두바로 키우기(해시 함수 바뀜)
- 테이블의 모든 원소를 다시 해싱하여 저장
- 보통 a를 0.5로 사용
3. 좋은 해시 함수 조건
- 계산이 빨라야함
- 키들을 모든 영역에 고루 분산시킬 수 있어야 함(키가 비슷하다고 더 가까이 놓으면 좋지 않음)
'[자료 구조 및 알고리즘]' 카테고리의 다른 글
| [자료구조 및 알고리즘] 그래프 (2) | 2024.12.07 |
|---|---|
| [자료구조 및 알고리즘] 균형 검색 트리 - AVL 트리 (0) | 2024.12.04 |
| [자료구조 및 알고리즘] 색인과 이진 검색 트리 (0) | 2024.12.03 |
| [자료구조 및 알고리즘] 고급 정렬 (0) | 2024.12.01 |
| [자료구조 및 알고리즘] 기본 정렬 (0) | 2024.12.01 |


